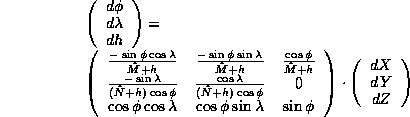Next: 4.2 Time
Up: IV. Physical
fundamentals
Previous:
IV. Physical fundamentals
- Appropriate, well defined and reproducable reference
coordinate systems are necessary for the description of satellite
motion,
observables and models.
- The increasing accuracy of many satellite observation techniques
requires the corresponding increase in the accuracy of reference
systems.
- Reference coordinate systems in satellite geodesy are global and
geocentric (Earth center of mass) by nature.
- Reference coordinate systems for terrestrial measurements are
local
and topocentric by nature.
- The relationship between global and local reference coordinate
systems might be know with an accuracy compatible with the accuracy
of the individual observations techniques: this is a goal.
- Some authors distinguish recently between:
- A reference system: the conceptual idea, including
the fundamental
theory and standards.
- A reference frame: the practical realization of
the reference
system through observations and a set of station coordinates (fiducial
stations).
4.1.1 Reference Coordinate Systems in
Satellite Geodesy
- Two systems are required:
- A space-fixed, inertial reference system (CIS) for the
description
of satellite motion, where the Newton's laws of motion are valid.
- An earth-fixed, terrestrial reference system (CTS) for the
positions
of the observations and for the description of results from satellite
geodesy.
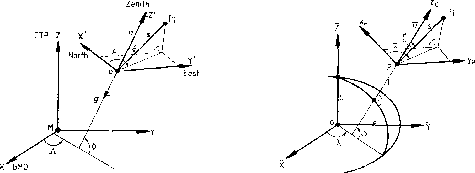
- A good approximation for a CIS is given by the quasi-inertial
equatorial system of the Astronomy (named in that way
due to the accelerations of the annual motion of the Sun around the
Earth).
- Its definition is:
- Origin: geocenter
- The positive Z-axis oriented towards the north pole
- The positive X-axis to the First Point of Aries (
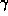 ).
).
- The Y-axis completes a right handed system
- The transformations between the associated spherical coordinates
right ascension
 , declination
, declination 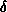 and geocentric distance r
with the cartesian coordinates X,Y,Z are:
and geocentric distance r
with the cartesian coordinates X,Y,Z are:
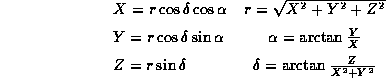
- The CIS reference frame was given by the fundamental stars FK5
(accuracy
of
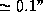 ) and
now for the HIPPARCOS output catalogue (
) and
now for the HIPPARCOS output catalogue (  ).
).
- A more precise definition (regarding to FK5) is given by means
of radiotelescopes with the VLBI technique, but in the recent pass
there were
not direct links between the two reference frames.
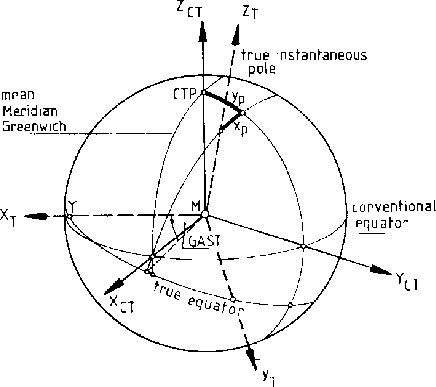
- The CTS (also named Earth Centered Earth Fixed System,
ECEF)
can be realized through a set of Cartesian coordinates of
fundamental stations within a global network, by means of the Conventional
Terrestrial Pole (CTP) and a zero longitude on the equator (Greenwich
Mean Observatory, GMO).
- The transformation from CIS to CTS is realized through a
sequence
of rotations that account for:
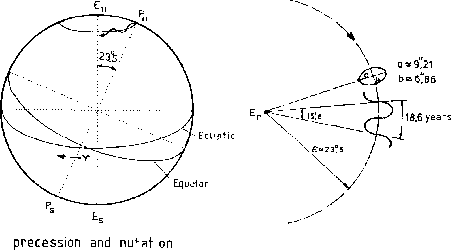
- Precession
- Nutation
- Earth rotation including polar motion

- The Earth's axis of rotation and its equatorial plane are not
fixed
in space, but rotate with respect to an inertial system, basically due
to the
gravitational attraction of the Sun and the Moon on the equatorial
bulge
of the Earth.
- The total motion is composed of a mean secular component
(precession:
mean equator, mean equinox and mean
positions)
and a periodic component (nutation: true equator, true
equinox
and true positions): one consequence is that the Earth
rotation axis
 describes an oscullating conic about the
ecliptic pole
describes an oscullating conic about the
ecliptic pole  .
.
- The mean positions can be transformed from the reference epoch
 (J2000) to the
required observation epoch t by means of the precession
rotation matrix:
(J2000) to the
required observation epoch t by means of the precession
rotation matrix:
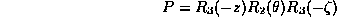
being the three rotation angles:
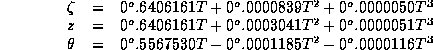
and 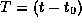 is counted in Julian centuries of 36525 days.
is counted in Julian centuries of 36525 days.
- The transformation from the mean equator and equinox to the
instantaneous
true equator and equinox for a given observation epoch:
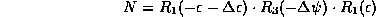
where  is the obliquity of the ecliptic,
is the obliquity of the ecliptic, 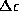 is the
nutation in obliquity and
is the
nutation in obliquity and 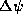 is the nutation in longitude counted
in the ecliptic:
is the nutation in longitude counted
in the ecliptic:
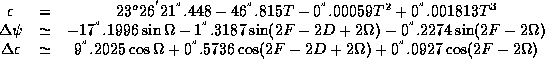
being 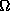 the mean longitude of the lunar ascending node and D
the
mean elongation of the moon from the Sun and
the mean longitude of the lunar ascending node and D
the
mean elongation of the moon from the Sun and 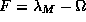 ....
....
- Finally we obtain the true coordinates
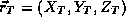 .
.
- For the transformation from an instantaneous space-fixed
equatorial
system to an conventional terrestrial reference system we need the
apparent Greenwich sidereal time (GAST) and the pole coordinates
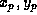 (these
are called Earth Rotation Parameters) -ERP- or
Earth Orientation Parameters -EOP-) that cannot be
described by theory:
they must be observed: astronomical observations, SLR to the satellites
and Moon, VLBI and GPS.
(these
are called Earth Rotation Parameters) -ERP- or
Earth Orientation Parameters -EOP-) that cannot be
described by theory:
they must be observed: astronomical observations, SLR to the satellites
and Moon, VLBI and GPS.
- So finally the matrix S that transform from the
instantaneous
space-fixed sytem to the CTS is:
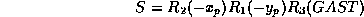
where
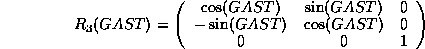
and (  are small angles):
are small angles):
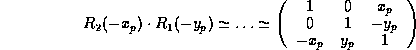
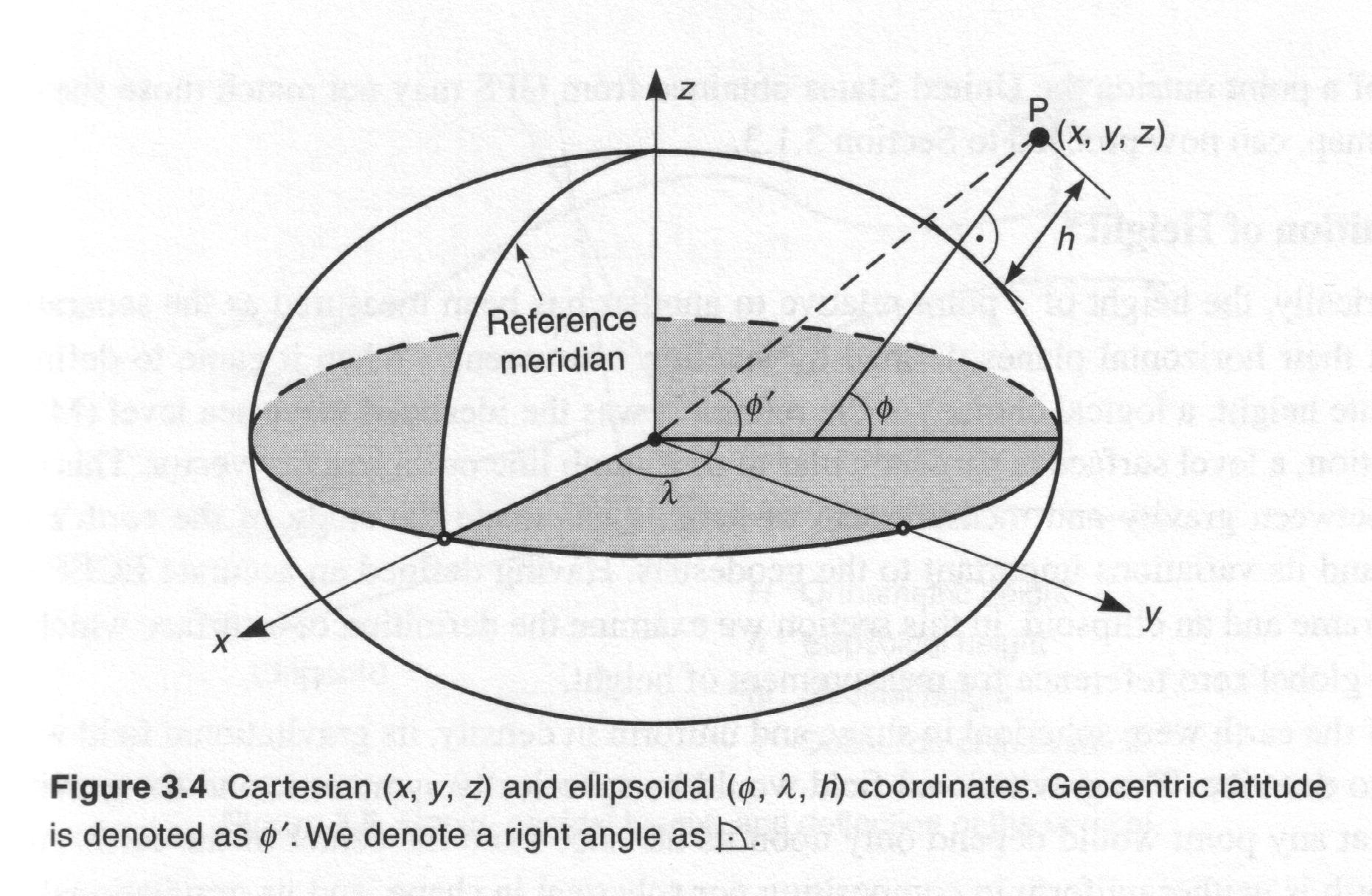
4.1.2 Ellipsoidal Reference Coordinate Systems
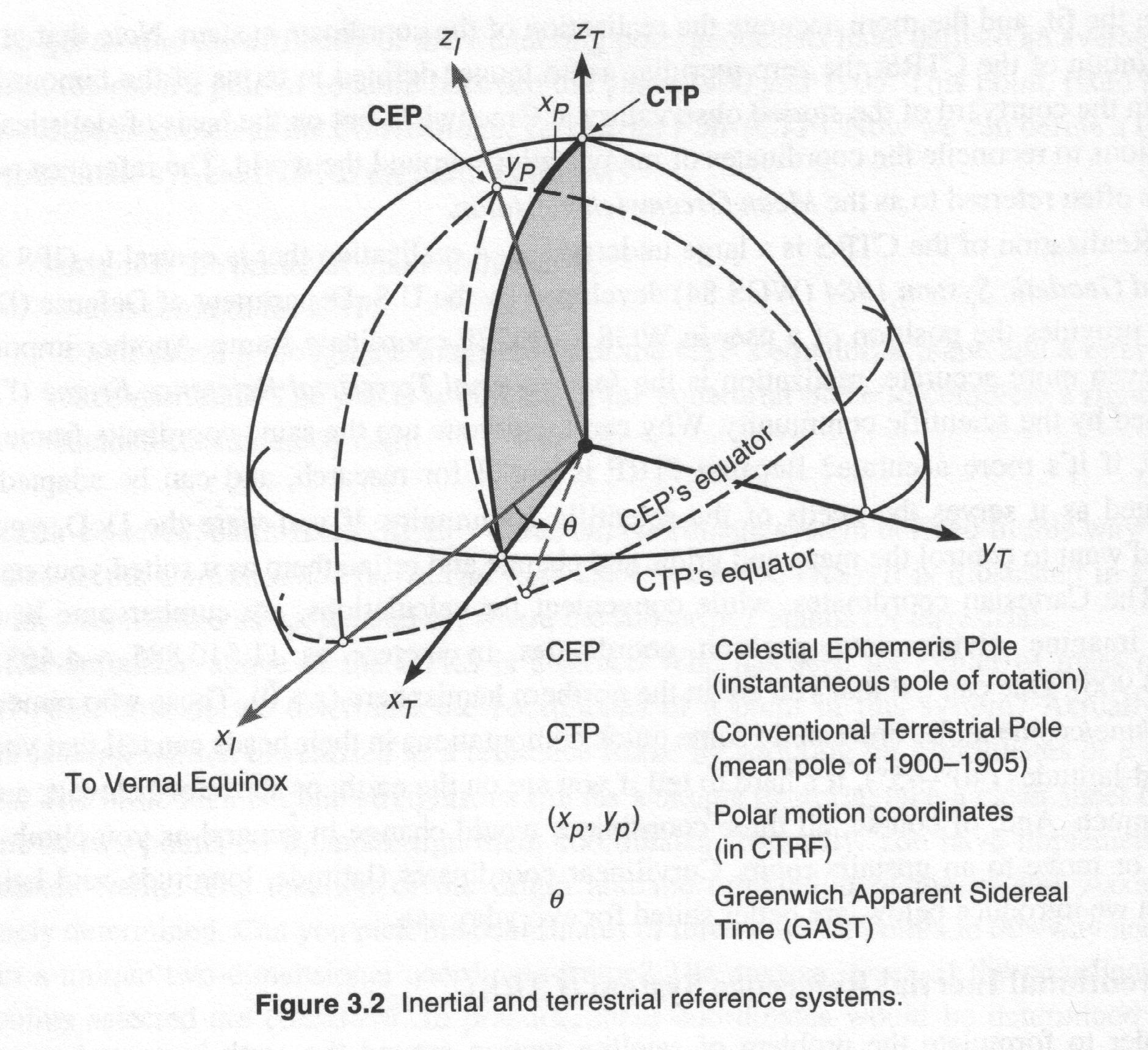
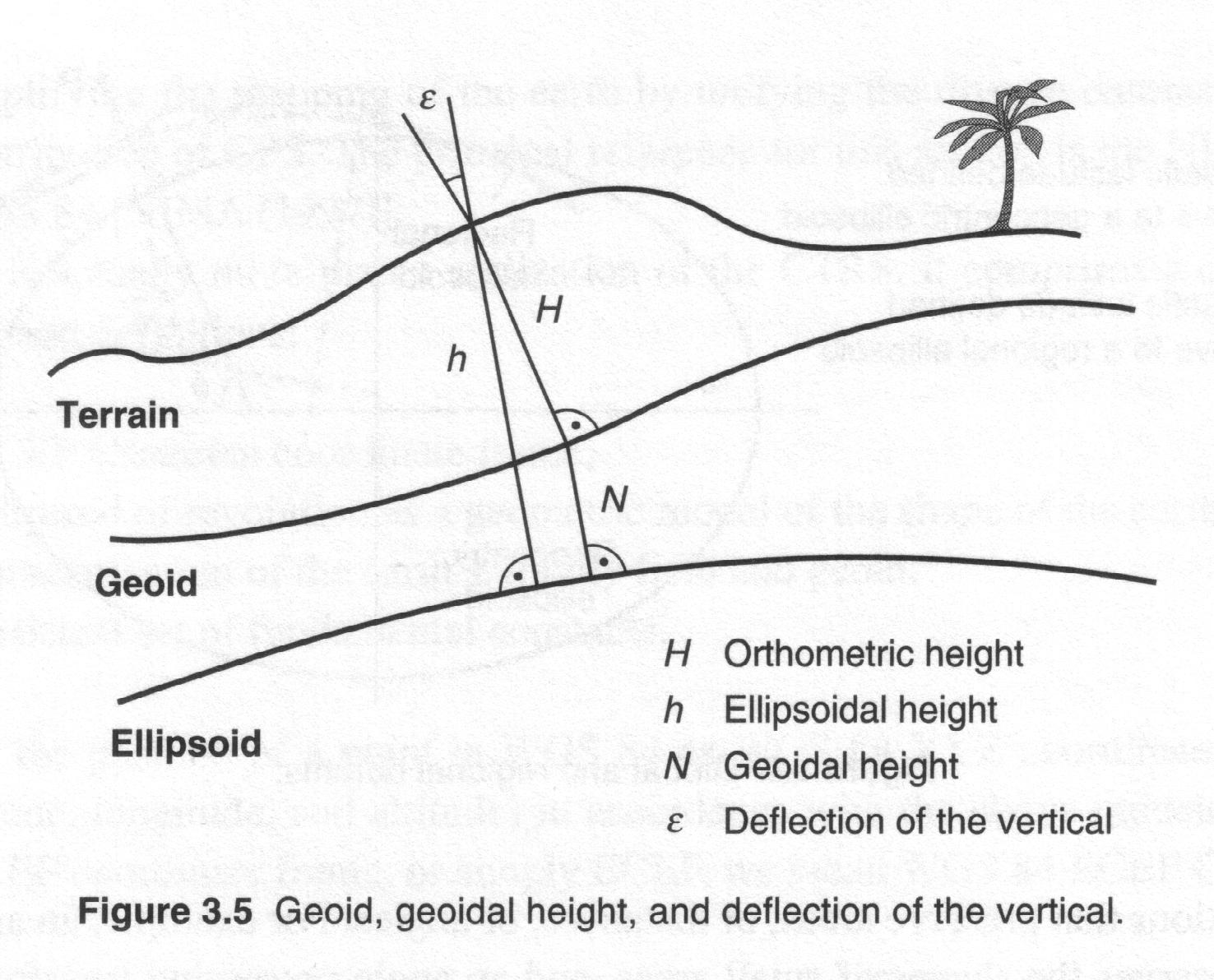
4.1.3 Ellipsoid, Geoid and Geodetic Datum
- The local ellipsoids are defined in such a way that
the
distributions of the known deflection of the vertical fulfilled some
minimum condition in the adjustment: the best fitting ellipsoids.
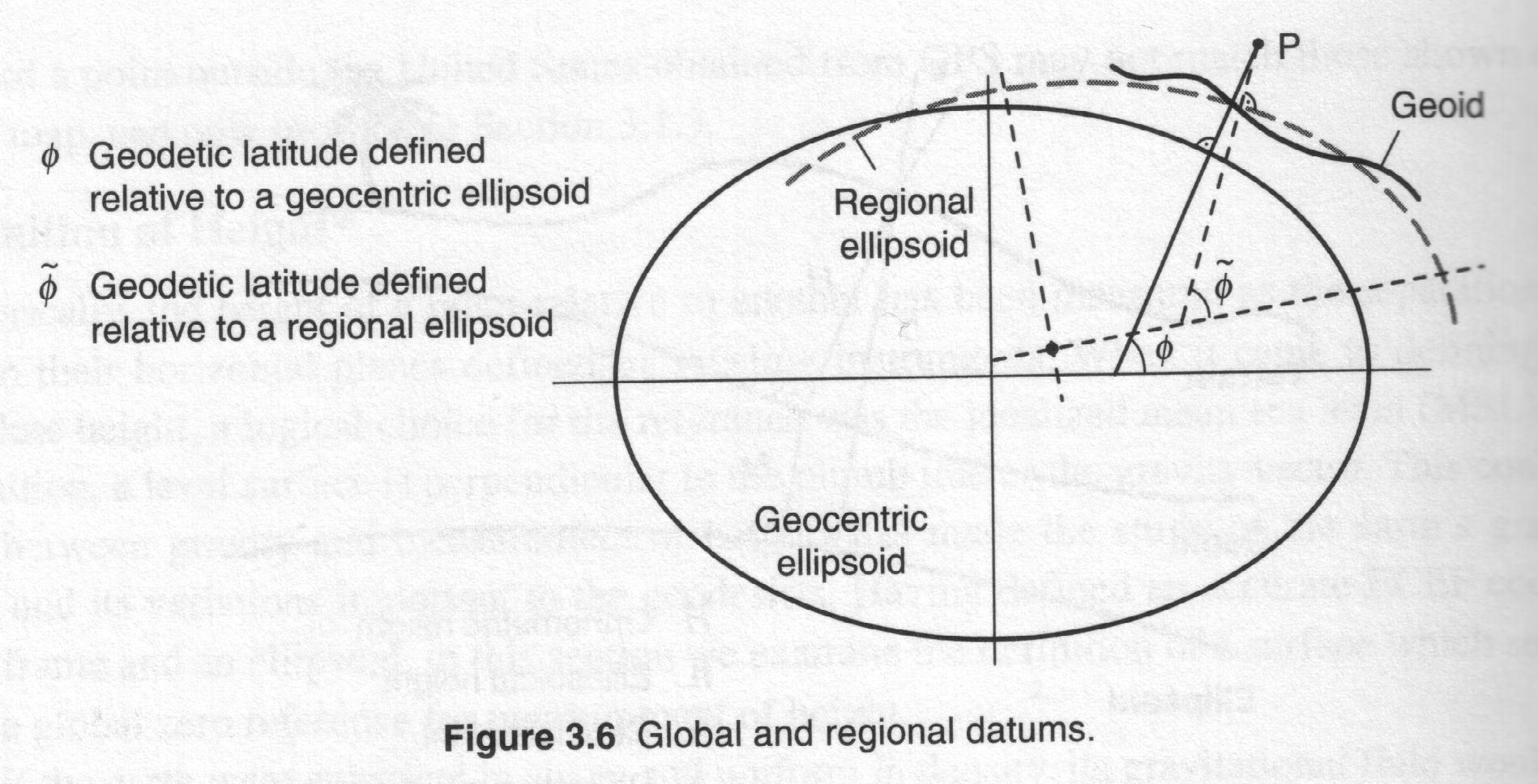
- A geodeticum datum: the set of parameters that
describe the
relationship between a particular local ellipsoid and a global geodetic
reference system. In general it is needed:
- 3 translation components
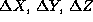 .
.
- 3 rotations
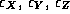
- 1 scale factor m
- Usually the rotation angles are very small:
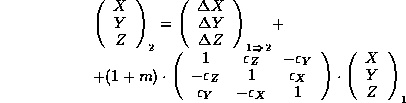
- When the datum information is derived from satellite orbits, the
potential coefficients of the Earth's gravity field as well as some
fundamental
constants (Earth rotation, velocity of light, geocentric gravitational
constants) form part of the datum definition:
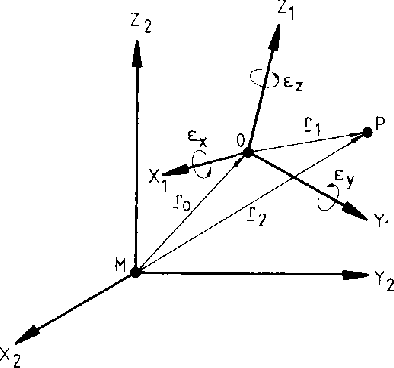
4.1.4 Three-dimensional Eccentricity
Computation
The transformations between eccentricity observations in ellipsoidal
coordinates ( 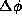 ,
, 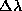 ,
, 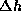 )
to the cartesian eccentricities (
)
to the cartesian eccentricities ( 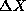 ,
, 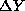 ,
,  ):
):
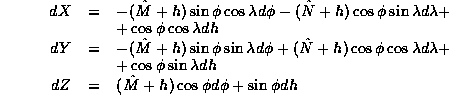
where 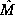 ,
,  are the
radius of curvature in the meridian and
in the prime vertical respectively:
are the
radius of curvature in the meridian and
in the prime vertical respectively:
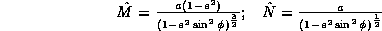
The inverse formula is:
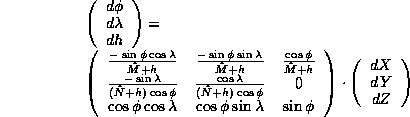



Next: 4.2 Time
Up: IV. Physical
fundamentals
Previous:
IV. Physical fundamentals
Manuel Hernandez Pajares
Thu Jun 4 14:25:37 GMT 1998


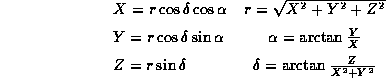
![]()
![]()
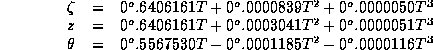
![]() is counted in Julian centuries of 36525 days.
is counted in Julian centuries of 36525 days.
![]()
![]() is the obliquity of the ecliptic,
is the obliquity of the ecliptic, ![]() is the
nutation in obliquity and
is the
nutation in obliquity and ![]() is the nutation in longitude counted
in the ecliptic:
is the nutation in longitude counted
in the ecliptic:
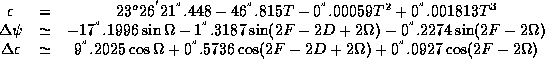
![]() the mean longitude of the lunar ascending node and D
the
mean elongation of the moon from the Sun and
the mean longitude of the lunar ascending node and D
the
mean elongation of the moon from the Sun and ![]() ....
....
![]()
![]()
![]() are small angles):
are small angles):
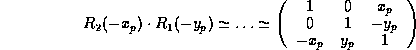



![]() is the radius of curvature in the prime vertical
is the radius of curvature in the prime vertical
![]()

![]()
![]()
![]()
![]()
![]()
![]() ,
, ![]() obtained from astronomical observations and
obtained from astronomical observations and ![]() ,
, ![]() from geodetic
observations.
from geodetic
observations.


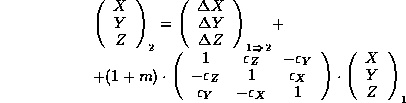
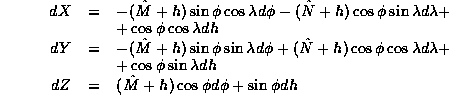
![]() ,
, ![]() are the
radius of curvature in the meridian and
in the prime vertical respectively:
are the
radius of curvature in the meridian and
in the prime vertical respectively:
![]()