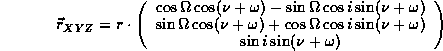Next:
3.4 Perburbed Satellite Motion
Up:
III. Satellite Orbital Motion
Previous:
3.2 Elliptic motion of
It can be show than only 6 of the 8 motion integrals obtained 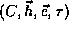 are
independent.
are
independent.
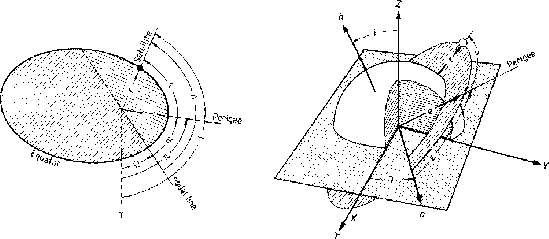
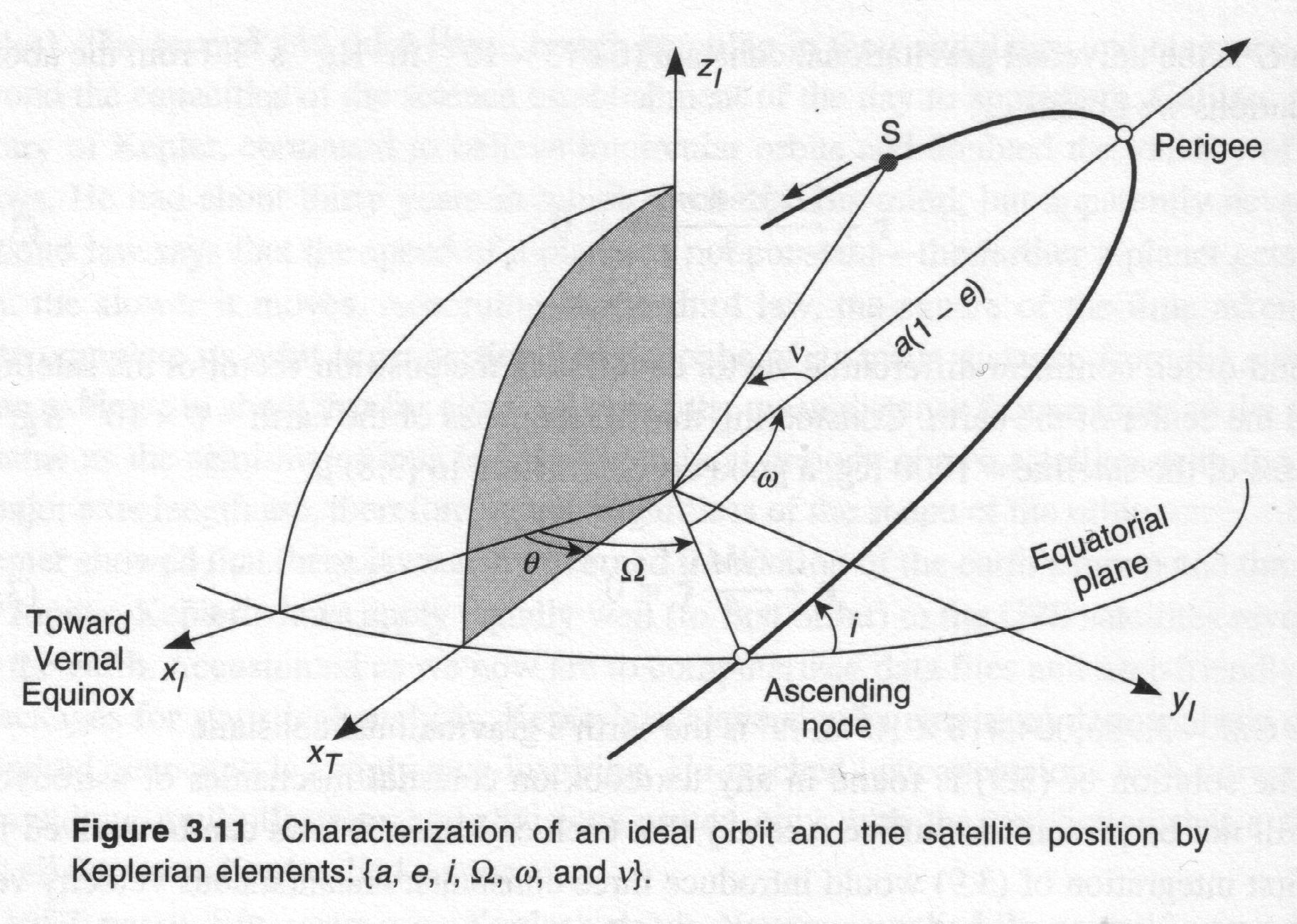
The motion integrals are usually expressed in terms of the orbital
elements,
defined as:
- Argument of the ascending node (
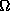 ): angle between the
X-axis and the direction of the ascending node, i.e. the point where
the
satellite cross the XY-plane (equator) with Z-velocity component
positive.
): angle between the
X-axis and the direction of the ascending node, i.e. the point where
the
satellite cross the XY-plane (equator) with Z-velocity component
positive.
- Orbit inclination (i): is the angle between the
orbit plane
and the XY-plane defined as the angle between the angular momentum
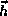 and the
Z-unitary vector
and the
Z-unitary vector 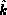 .
.
- Perigee argument (
 ): angle between the perigee
): angle between the perigee 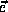 and the
ascending node direction, extended on the orbital plane.
and the
ascending node direction, extended on the orbital plane.
- Eccentricity (e).
- Perigee pass epoch (
 ).
).
- Major semiaxis (a).
From equations 2,4 and 5:

and

From the orbital elements is posible to compute the position and
velocity
of the satellite in any epoch t:
- The mean anomaly
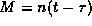 is computed.
is computed.
- By means of the Kepler equation 10 we estimate (iteratively)
the mean anomaly E:

- Now, with equations 7, 8, we get the geocentric
satellite distance and the true anomaly, r and
 :
:

- From the polar coordinates in the orbit plane, we have to
perform
several rotations to get the coordinates in the equatorial reference
frame:
- Z-rotation of angle
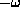
- X-rotation of angle -i (following the new X axis)
- Z-rotation of angle
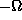 (following the new Z axis)
(following the new Z axis)
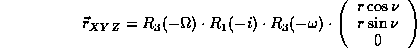
To get finally:
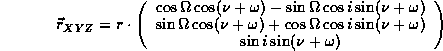
Manuel Hernandez Pajares
Thu Jun 4 14:25:37 GMT 1998
![]() are
independent.
are
independent.


![]()
![]()
![]()
![]()
![]()