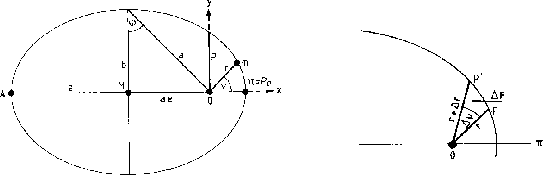
We are going to express the temporal dependence of the satellite motion in the orbit.
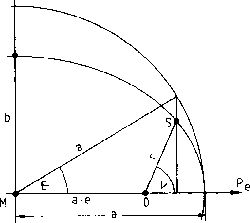
The parametric equation of the ellipse referred to one of the focus can be written as:
being E the eccentric anomaly (see figure), a major semiaxis,
and b the minor semiaxis 
.
The distance of the satellite to the Earth center from equation 3.2 is:
and dividing both components also from equation 3.2:
And the angular momentum can be written as:
Taking into account that if n is the mean angular velocity of the satellite along one orbit and h/2 is the constant area velocity:
And from the last two relationships the Kepler equation is obtained
being 
the perigee pass time and n the mean angular velocity:
. The term 
is known as mean anomaly.
Finally, from equations 9 and 6 we can get the third
Kepler law:
where T is the orbit period.
